|
The pictures on either side of this text reproduce some of Maryam Mirzakhani's diagrams together with natural forms.
There is a theme of hyperbolic shapes. They are found in nature, like the surface of the shell on the left, or as abstract surfaces parametrised locally by complex numbers. On the right, the upper inked shapes are equivalent to the lower drawn one cut in the two places shown by a circle with a dashed line on the underside. This diagram was adapted from fig. 2 from Mirzakhani, M. (2008) "Growth of the number of simple closed geodesics on hyperbolic surfaces." Annals of Mathematics p112. |
The three images above reference mathematical roots that are foundational to Maryam Mirzakhani's work.
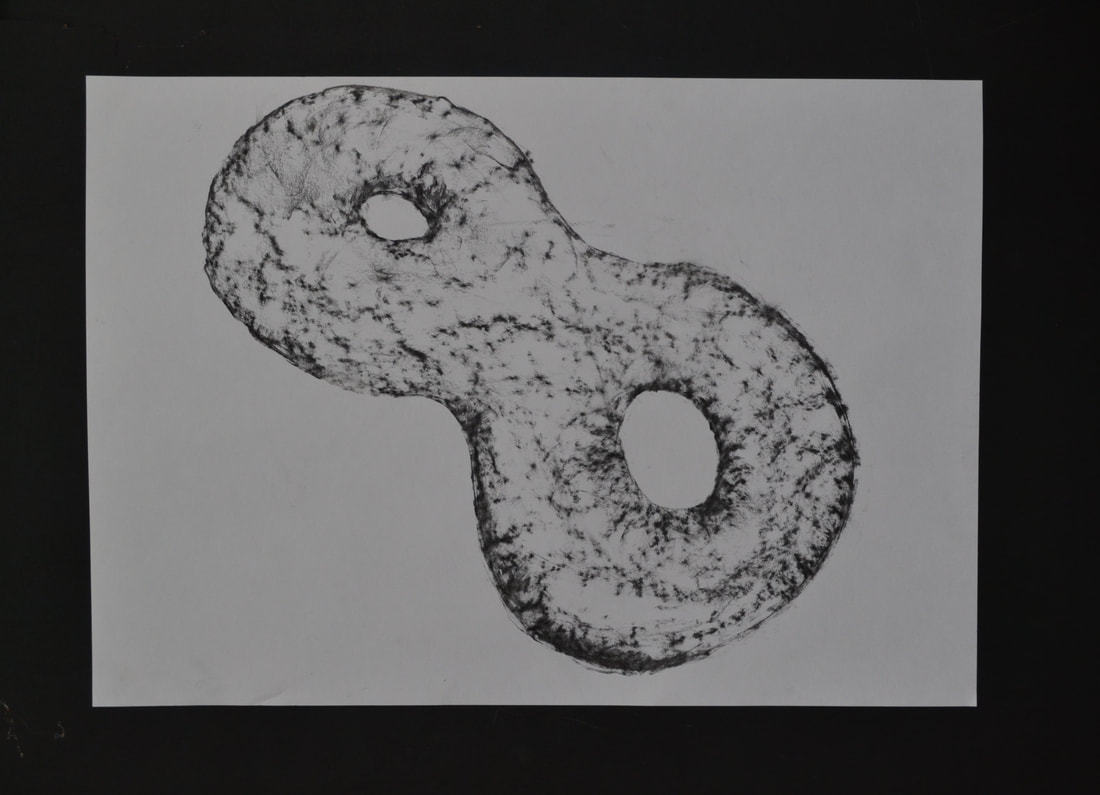
On the left, the image, real and imaginary, is referencing the notion of a complex number z=x+iy which has a 'real number' part, x, and an imaginary part, iy, the term i can be thought of as a rotation through 90degrees (anti-clockwise) and -1 is a rotation through 180degrees. The image is made with the real pieces of wood rotated through 90degrees and 180degrees respectively from the piece's painted image. The superimposed photo is of the work in progress, is it real or imaginary? The central image is a drawing of a two holed torus. When such shapes are parametrised by complex numbers (such that they are compact Riemann surfaces of negative curvature) they cannot exist in 3dimensional space, which is pretty imaginary though 'real', in the sense that it has been proved. Curves on these sort of Riemann surfaces were studied by Mayam Mirzakhani. The image on the right, billiard balls, references a real representation of curves on such surfaces as the paths of abstract billiard balls. Topics to study include 'how many straight (geodesic) paths are there?', 'what paths are simple loops?', 'how does the surface constrain the curves?'.
On the left, the image, real and imaginary, is referencing the notion of a complex number z=x+iy which has a 'real number' part, x, and an imaginary part, iy, the term i can be thought of as a rotation through 90degrees (anti-clockwise) and -1 is a rotation through 180degrees. The image is made with the real pieces of wood rotated through 90degrees and 180degrees respectively from the piece's painted image. The superimposed photo is of the work in progress, is it real or imaginary? The central image is a drawing of a two holed torus. When such shapes are parametrised by complex numbers (such that they are compact Riemann surfaces of negative curvature) they cannot exist in 3dimensional space, which is pretty imaginary though 'real', in the sense that it has been proved. Curves on these sort of Riemann surfaces were studied by Mayam Mirzakhani. The image on the right, billiard balls, references a real representation of curves on such surfaces as the paths of abstract billiard balls. Topics to study include 'how many straight (geodesic) paths are there?', 'what paths are simple loops?', 'how does the surface constrain the curves?'.
in memory of Maryam Mirzakhani